Volo in salita

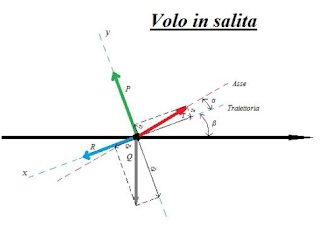
Per lo studio del volo in salita idealizziamo uno schema dove le forze applicate al velivolo si concentrano nel suo baricentro e si sviluppano lungo assi perpendicolari tra loro.

Si ha come riferimento fisso la linea dell'orizzonte, la quale forma con la traiettoria seguita dal velivolo un angolo definito "di rampa" e nominato β. Quest'ultimo non va confuso con l'angolo α, definito invece come quello compreso tra la traiettoria e l'asse del velivolo.

Parlando ora delle forze che agiscono sul corpo in questione si avrà una forza peso Q sempre perpendicolare all'orizzonte orientata verso il basso e una portanza P sua opposta che agisce su di un asse y formando un angolo di 90° con la traiettoria, la quale coincide quindi con l'asse x e ospita la resistenza R, orientata in maniera opposta rispetto alla trazione T che invece si estende lungo l'asse del velivolo.

Per l'analisi delle stesse e della loro risultante è necessario scomporre quelle non agenti su assi paralleli nei corrispondenti vettori agenti sugli assi x e y. Si identificheranno quindi Tx, Ty, Qx e Qy.

Avendo come scopo principe l'ottenere i valori reali delle forze disegnate si procede alla somma vettoriale delle stesse sui due assi:

Applicando le regole goniometriche di seno e coseno e degli angoli opposti (per la quale l'angolo compreso tra l'asse di azione della forza Q e l'asse y è uguale a β) si ha che:

Considerando poi α ≃ 0 otteniamo  come equazioni semplificate del volo in salita le seguenti:

Esistono poi due casi particolari del volo in salita, siano essi il volo in salita rapida e in volo in salita ripida.
Si distinguono per l'anormale assetto di volo che nel primo corrisponde all'assetto di massima salita, e nel secondo all'assetto di massima pendenza.

Analizzando più nello specifico i due casi notiamo che per il volo in salita ripida:

• l'angolo di rampa β è massimo;
• la velocità di riferimento è quindi Vβmax ;
• assetto di massima pendenza  = Cpmax 

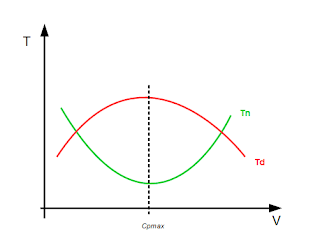
Il grafico seguente pone in relazione T (trazione) e V (velocità) individuando due curve di andamento opposto Tn (trazione necessaria) e Td (trazione disponibile) il cui divario calcolato sull'asse y è detto supero di trazione. Quando quest'ultimo è massimo si individua l'assetto di pendenza massima, corrispondente all'assetto a Cpmax.

Per il volo in salita rapida invece si ha che:

• la salita avviene nel minor tempo possibile (tmin) e a Vmax;
• La velocità si ottiene dalla formula V =
• assetto di salita massima = 

Anche per questo tipo di volo esiste in grafico in grado di individuare il punto in cui l'assetto dell'aereo corrisponde a quello di salita massima. Si tratta di un grafico portanza-velocità che descrive due curve rappresentanti la potenza necessaria (Pn) e la potenza disponibile (Pd). Come nel grafico precedente il divario tra le due curve è detto supero, questa volta di potenza, e quando esso è massimo individua nel grafico il punto di assetto di salita massima, anche corrispondente all'assetto a