SOLLECITAZIONI E DIMENSIONAMENTO
Esistono due tipi di sforzi: σ (sigma), che agiscono in maniera perpendicolare alla superficie, e 𝜏 (tau), che sono invece sforzi tangenziali. Questi due sforzi, isolati o combinati, possono originare i seguenti sollecitazioni:
Ai fini del dimensionamento della sezione resistente, è necessario determinare σ (sigma ammissibile), solitamente uguale o minore a un valore tra sigma di rottura (materiali fragili) e sigma di snervamento (materiali duttili). In particolare, da 𝜎AMM si ricava 𝜎AMS (sigma ammissibile statica) mediante i coefficienti n(vd. tab.1) con la seguente formula:
Esistono due tipi di sforzi: σ (sigma), che agiscono in maniera perpendicolare alla superficie, e 𝜏 (tau), che sono invece sforzi tangenziali. Questi due sforzi, isolati o combinati, possono originare i seguenti sollecitazioni:
- Sforzo normale
- Taglio
- Momento flettente
- Momento torcente
Ai fini del dimensionamento della sezione resistente, è necessario determinare σ (sigma ammissibile), solitamente uguale o minore a un valore tra sigma di rottura (materiali fragili) e sigma di snervamento (materiali duttili). In particolare, da 𝜎AMM si ricava 𝜎AMS (sigma ammissibile statica) mediante i coefficienti n(vd. tab.1) con la seguente formula:
Nei calcoli successivamente descritti, si utilizzerà la 𝜎AMS (senza applicazione di fatica).
SFORZO NORMALE
Gli sforzi normali sono trazione (tensione delle fibre) e compressione (le fibre sono compresse). Sigma è costante su tutta la sezione resistente, per cui si applica la seguente formula:
in cui N è la sollecitazione normale, e A è la sezione resistente. Quindi si ricava A:
Se la sezione è circolare, è possibile ricavare il diametro:
Se invece la sezione ha forma rettangolare, è necessario stabilire una relazione tra base e altezza della sezione.
MOMENTO FLETTENTE
Il momento flettente è una sollecitazione generata come effetto di forze perpendicolari σ applicate ad certa una distanza (braccio) da un punto di applicazione P. Non essendo il momento flettente uguale per tutte le sezioni della trave (dipende dal braccio), è necessario identificare quella con Mf maggiore. Tuttavia, sigma non è uniforme su tutta la superficie, pertanto bisogna considerare i punti critici in cui vi è maggiore sollecitazione. Per il dimensionamento, si deve conoscere Wx (modulo di resistenza assiale), ricavabile dalla formula seguente:
in cui Mf è il momento flettente. S calcola dalla formula inversa Wx:
Wx è esprimibile come:
da cui si può ricavare il diametro (considerando sezioni circolari):
Per quanto riguarda le sezioni rettangolari, è sufficiente stabilire una relazione tra base e altezza, e applicare la seguente formula:
TAGLIO
La sollecitazione di taglio consiste nell' applicazione di forze tangenziali 𝜏 alla superficie della trave. I corpi soggetti a taglio si considerano rigidi e indeformabili (non si genera momento flettente).
Come per il momento flettente, lo sforzo di taglio non è uguale per tutte le sezioni (occorre individuare la sezione maggiormente sollecitata per procedere al dimensionamento), né 𝜏 è uniforme per un' intera sezione (è massimo in corrispondenza dell' asse baricentrico).
Per conoscere i valori di 𝜏AMS di un materiale ci si avvale della seguente formula:
e in particolare:
(notare che i coefficienti n (tab. 1) sono validi sia per gli sforzi 𝜏 che σ)
Ai fini del dimensionamento, è necessario determinare un valore 𝜏 massimo che soddisfi la seguente relazione:
Conoscendo 𝜏MAX si calcola 𝜏 medio su cui si basa il dimensionamento. Per le sezioni circolari, 𝜏MED vale:
mentre per le sezioni rettangolari si usa la seguente formula:
Si ricava quindi l' area della sezione dalla formula:
che diventa:
Ora è possibile calcolare il diametro in caso di sezioni circolari:
per le sezioni rettangolari è necessario stabilire una relazione tra base e altezza.
MOMENTO TORCENTE
Il momento torcente è una sollecitazione generata da sforzi tangenziali 𝜏 per i quali su una sezione della trave si crea un momento direttamente proporzionale alla distanza dal baricentro della sezione. Si analizzeranno solo sezioni circolari.
I calcoli del dimensionamento vengono effettuati facendo riferimento al valore 𝜏:
in cui 𝜏AMS si ottiene con la formula precedentemente utilizzata per i calcoli del taglio.
Si procede calcolando il parametro Wp (modulo di resistenza polare) dalla seguente formula:
Wp è anche esprimibile come:
da cui è ricavabile il diametro d:
SOLLECITAZIONI COMPOSTE:
Le sollecitazioni composte sono il risultato dell' applicazione di due o più sollecitazioni semplici. Si approfondiranno due dei casi più frequenti:
- Pressoflessione
- Flessotorsione
PRESSOFLESSIONE
E' il caso in cui si applicano sollecitazioni di compressione e di flessione (momento flettente). Dato che si tratta di forze complanari (sforzi sigma), essi si sommano algebricamente per ottenere lo sforzo complessivo 𝜎ID (𝜎 ideale). 𝜎ID viene posto minore o uguale alla sigma ammissibile statica:
𝜎ID è dunque pari a:
Sviluppando questa formula se ne ottiene un' altra tramite la quale è possibile calcolare le dimensioni della sezione resistente. Non è però applicabile direttamente la sua formula inversa, in quanto non è possibile risolvere equazioni polinomiali di grado superiore al secondo: risulta dunque necessario procedere per tentativi, assumendo valori dimensionali tali per cui risulti vera la relazione tra 𝜎ID e 𝜎AMS.
FLESSOTORSIONE
In questo caso gli sforzi agenti sono sia sigma (flessione) che tau (torsione) pertanto, dato che non si tratta di forze parallele tra loro, è necessario applicare un metodo analogo al teorema di Pitagora per le somme vettoriali: il criterio di tresca, che si presenta come:
in cui il risultato è sempre un valore di sigma ideale, che viene imposto minore o uguale a 𝜎AMS.
Sviluppando la precedente formula, si ottiene:
Wp è esprimibile come:
Sostituendo, si ottiene:
Si identifica quindi il valore Mfeq:
è possibile infine conoscere i valori dimensionali applicando la formula per il calcolo del diametro espressa nella sezione del momento flettente. Per fare ciò si calcola Wx come:
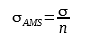








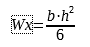

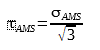





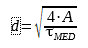







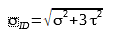





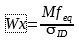
Commenti
Posta un commento